Uno de los momentos más emocionantes y reconfortantes de los entrenadores sucede cuando nuestros atletas logran un récord personal. Es como si nosotros mismos lo estuviéramos consiguiendo, y la sensación de “mi esfuerzo vale la pena” es alimento para nutrir también nuestro ego.
Pero, ¿y si malinterpretamos el verdadero progreso del atleta? Una vez, un entrenador dijo: “cualquiera puede ser un gran entrenador con un mal uso de las estadísticas”.
En ese sentido, en el campo de las ciencias del deporte, el análisis de inferencia basado en magnitud (IBM) es uno de los temas estadísticos más relevantes. Asimismo, el entrenamiento basado en la velocidad (VBT) es un método que hoy, prácticamente todos los entrenadores de fuerza han incorporado a sus programas, y además, es muy preciso para estimar 1RM.
En esta entrega nos explayaremos sobre el VBT, el IBM y muchos otros conceptos como medición perfecta, valor verdadero, error, incertidumbre o cambio más pequeño significativo, siempre enfocados en cómo evaluar y seguir con precisión el progreso de nuestros atletas.
Valor verdadero, error, incertidumbre, distribución de probabilidad
Consideremos los resultados obtenidos de una medición. Si pudiéramos hacer una medición “perfecta”, obtendríamos el “valor verdadero”. Sin embargo, la realidad es que las mediciones que hacemos nunca son perfectas, y los valores obtenidos de la medición son, por lo tanto, aproximaciones a este “valor verdadero”.
Un valor medido diferirá del hipotético “valor verdadero” por varias razones diferentes, algunas de las cuales podemos conocer, y otras no.
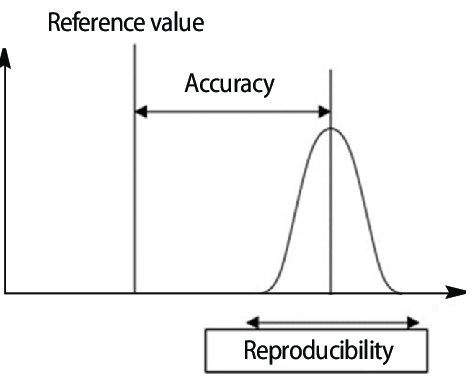
Llamamos error a la diferencia entre el valor medido y el “valor verdadero”, y cuanto más cerca esté uno del otro, más precisa será nuestra medición.
Por definición, nunca podemos saber el “valor verdadero” exacto y, sin él, tampoco podemos saber la diferencia exacta entre él y las mediciones que hicimos. Conocer el valor exacto de un error también es imposible. Sin embargo, podemos describir el error en el resultado de una medición particular, como un dibujo de una distribución de probabilidad.
La incertidumbre asociada a un valor medido es una medida de esa distribución de probabilidad. En concreto, la incertidumbre estándar es la desviación estándar de esta distribución de probabilidad. Esto significa que cuanto mayor sea la variabilidad de un conjunto de datos, mayor será la incertidumbre y el error que tendremos.
Todo el mundo está familiarizado con las evaluaciones de 1RM, que a menudo se consideran el “patrón oro” para evaluar la capacidad neuromuscular de los individuos, en entornos que no son de laboratorio.
Realizar un protocolo de 1RM probablemente nos dará mayor precisión, pero por otro lado, es un proceso que consume mucho tiempo, genera fatiga en el atleta y se ve afectado por factores internos (por ejemplo, se ha demostrado que los ritmos circadianos alteran significativamente el rendimiento) y externos, como la retroalimentación verbal del entrenador o incluso la música.
A su vez, no podemos realizar la prueba diariamente, por lo que tal vez no detectemos mejoras o disminuciones, debido al marco temporal en el que se aplica la prueba. Por lo tanto, estamos perdiendo la oportunidad de ajustar el plan a tiempo.
Por el contrario, al estimar el valor de 1RM y, si elegimos el método apropiado, estamos ganando en practicidad, simplicidad, tiempo, y posibilitando períodos más cortos (diarios, semanales), sin afectar el proceso normal de entrenamiento, pero a expensas de una mayor “incertidumbre” y “error”, aunque de verdad podríamos reducirlo.
Así pues, si hipotéticamente hacemos una prueba (o calculamos) 1RM el mismo día con el mismo atleta, sin el efecto de interferencia de una prueba con las demás, vamos a obtener 3 valores diferentes, una media y una variabilidad (SD) determinada.
La cuestión es: ¿cómo podemos estar seguros de que las diferencias son mejoras “reales” (señal) y no la variación normal de los datos (ruido)?
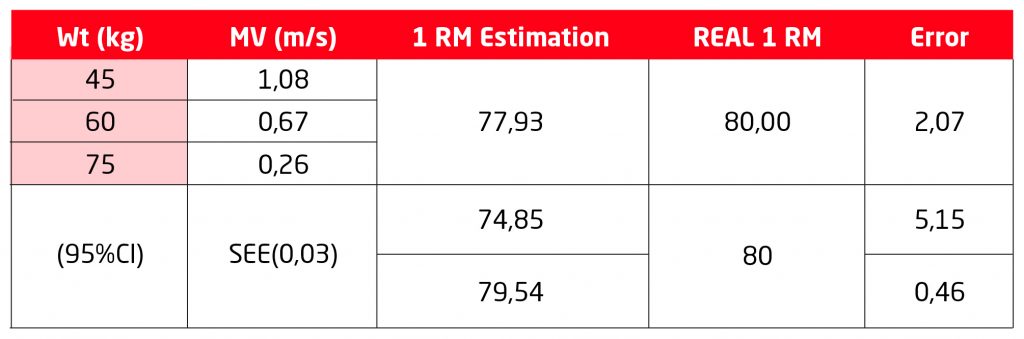
Estimación de 1 RM usando VBT
Las sesiones programadas de evaluaciones han quedado atrás, excluyendo los deportes de fuerza (aún incluso ahí). Los entrenadores de hoy en día no se pueden permitir dedicar un día entero a evaluar, especialmente en los deportes de equipo que compiten todos los fines de semana.
Pero la esencia de las pruebas es monitorear tanto las cargas de entrenamiento como los efectos del mismo, sin afectar el proceso normal de entrenamiento, ayudándonos a modificarlo en caso que fuera necesario.
En el pasado, aunque existía el entrenamiento basado en la velocidad (VBT), sólo se utilizaba para la investigación, principalmente debido a los costes de los dispositivos. Pero en la última década, la rápida difusión y la creciente asequibilidad de los transductores lineales contribuyeron a la realidad actual, en la que prácticamente todos los entrenadores de fuerza actualizados incorporan el VBT en sus programas.
El uso del VBT ha demostrado ser una forma realmente precisa de estimar 1RM, debido a la relación matemática lineal y estable (inversamente correlacionada, con coeficientes de correlación de > 0,95) que existe entre la carga y la velocidad concéntrica media a la que se mueve dicha carga; al menos, es tan buena como el método de repeticiones hasta el fallo.
Además, el método de dos puntos ha surgido recientemente como un procedimiento válido, factible, rápido y libre de fatiga, para la evaluación de las relaciones fuerza-velocidad y carga-velocidad, que sólo necesita realizar 2 cargas externas diferentes, que representan aproximadamente el 50 y el 80% de 1RM para obtener un perfil L-V.
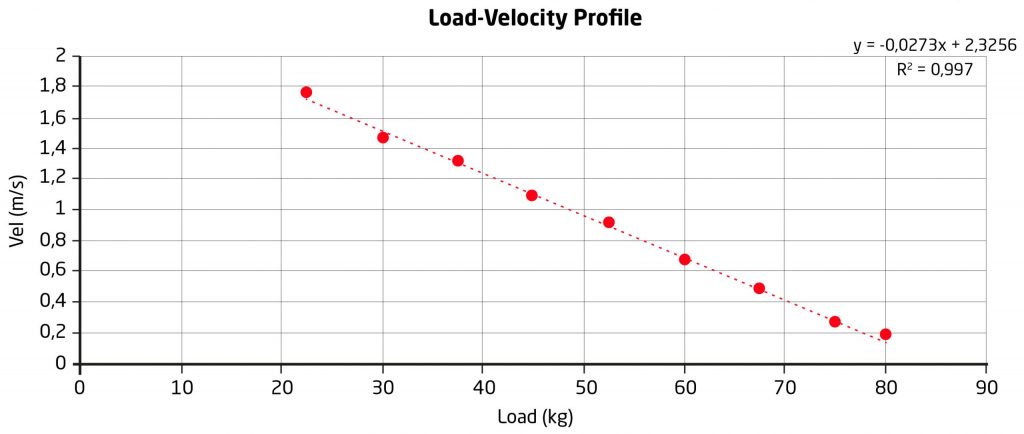
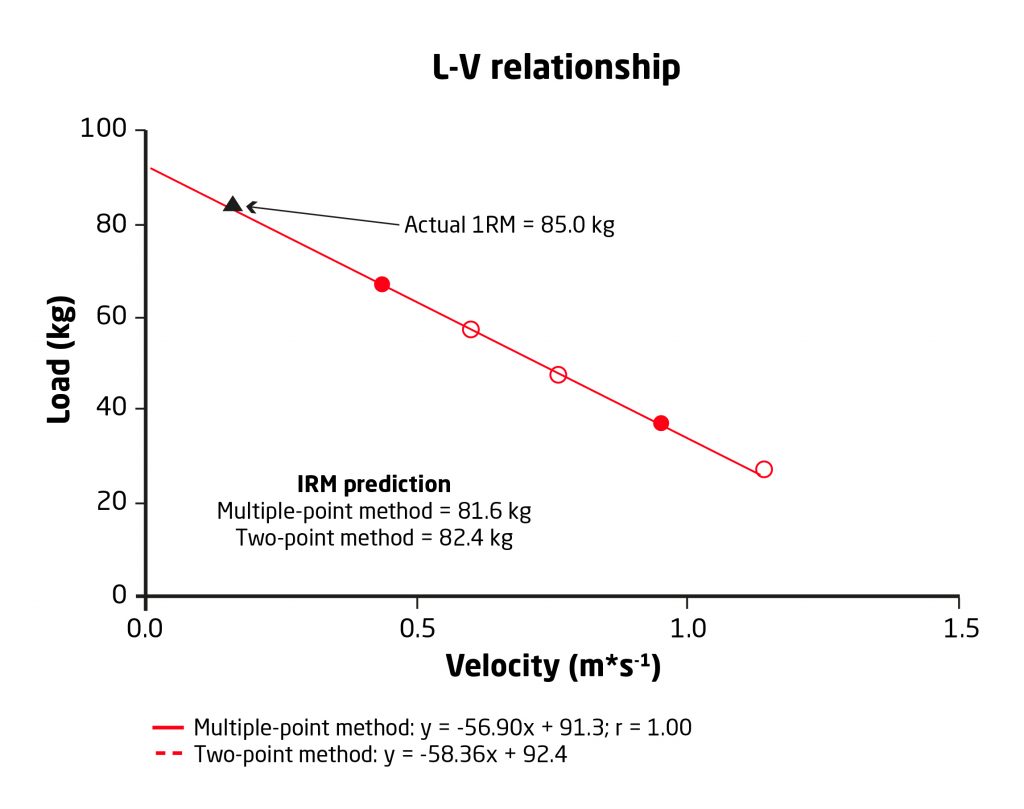
Sin embargo, es necesario considerar algunas cosas:
- Los ejercicios tradicionales como las sentadillas, press de banca, el peso muerto, etc, tienen su propia velocidad de carga (L-V). Esto significa que necesitamos establecer el perfil L-V para un determinado atleta, y el ejercicio que realice antes de estimarlo con cargas submáximas a diario.
- La relación L-V es más sensible a la velocidad media o a la velocidad media de propulsión, que la velocidad máxima en los ejercicios tradicionales.
- El dispositivo debe ser válido y fiable.
- Los intentos de carga máxima se asocian a una velocidad específica que se conoce como “umbral de velocidad mínima (MVT, “minimal velocity threshold)”.
- Esto significa que la velocidad media de la 1RM no será significativamente diferente, desde el punto de vista estadístico, de la velocidad media de la última repetición de una RM dada (5RM, 3RM, etc).
- Hay muchas investigaciones sobre los diferentes ejercicios y sus MVT (por ejemplo, la prensa de banco y la sentadilla suelen estar alrededor de 0,13 – 0,3 m/s respectivamente).
- Los mayores %RM relativos son más fuertes predictores del 1RM real que los menores. La carga de 5RM es menos precisa que la carga de 3RM para estimar 1RM.
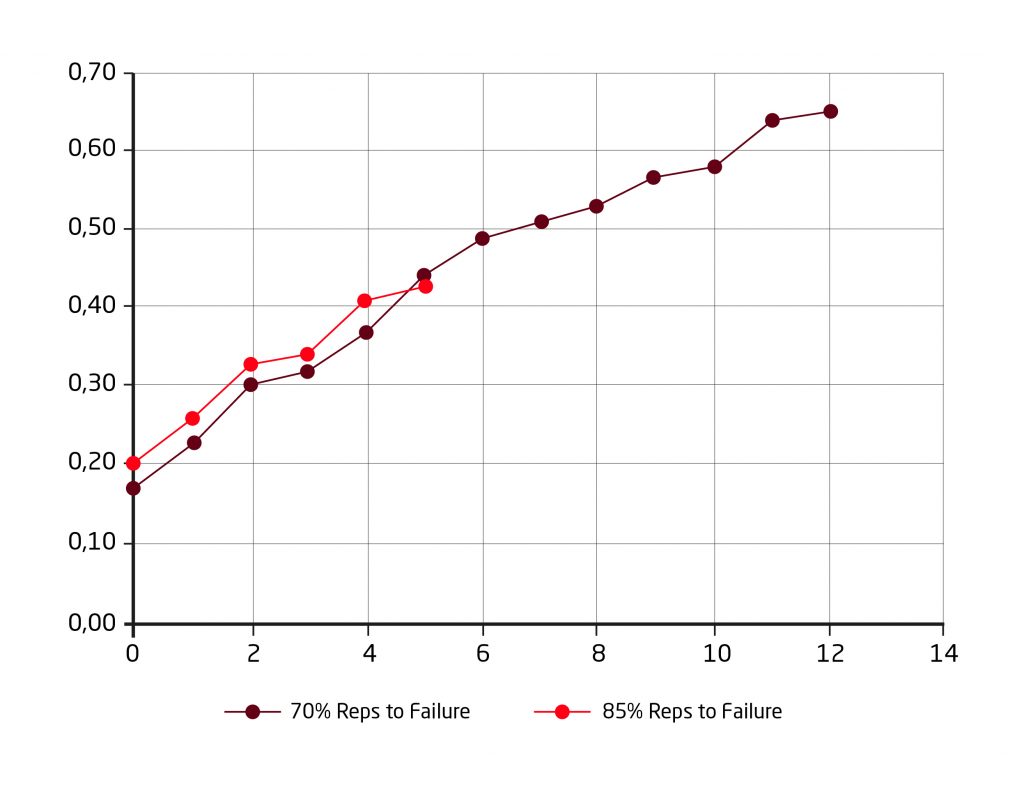
Por lo tanto, una vez que conocemos el perfil L-V de un determinado atleta y un ejercicio en concreto, así como el MVT, estamos listos para comenzar.
Inferencia basada en la magnitud
El IBM se basa en la labor de los profesores William Hopkins y Alan Batterham, y trata de abordar algunas de las deficiencias que puede generar el uso de los enfoques estadísticos tradicionales, ayudando a identificar las diferencias y a optimizar el proceso de toma de decisiones.
Los científicos deportivos y los entrenadores tratan por lo general con pequeños grupos de atletas (para recopilar y analizar datos como en los entornos deportivos de campo), e incluso con N=1, como en el levantamiento de pesas, el atletismo, y también en los deportes de campo donde el análisis de los cambios individuales a lo largo del tiempo se vuelve crucial.
Además, a veces los pequeños cambios merecen la pena, aunque las diferencias no sean relevantes desde el punto de vista estadístico (¿cuántos milisegundos separan al ganador de los perdedores en una final olímpica de sprint de 100mts, o cm en un lanzamiento o kg en una competición de levantamiento de potencia o de pesas?).
Las estadísticas tradicionales no van bien ni con pequeñas muestras ni con pequeñas diferencias para dar información relevante. Una de las piedras angulares del IBM es la definición del [cambio más pequeño significativo], o [Smallest worthwhile change] (SWC).
Es crucial entender qué es realmente el cambio. El cambio se relaciona muy íntimamente con el concepto de diferencia; es decir, el cambio se juzga en base a una diferencia en alguna entidad medible y casi siempre se relaciona con un lapso de tiempo.
Por ejemplo, si debido al entrenamiento, un atleta aumenta su 1RM de 110 a 150 en 6 semanas, esto será considerado como un cambio positivo. El principio básico es que, cuando se abarcan días o semanas, las mediciones de la misma variable difieren de una sesión de prueba a otra.
No obstante, como ya hemos revisado, estamos tratando con mucha incertidumbre, especialmente cuando las diferencias no son tan grandes.
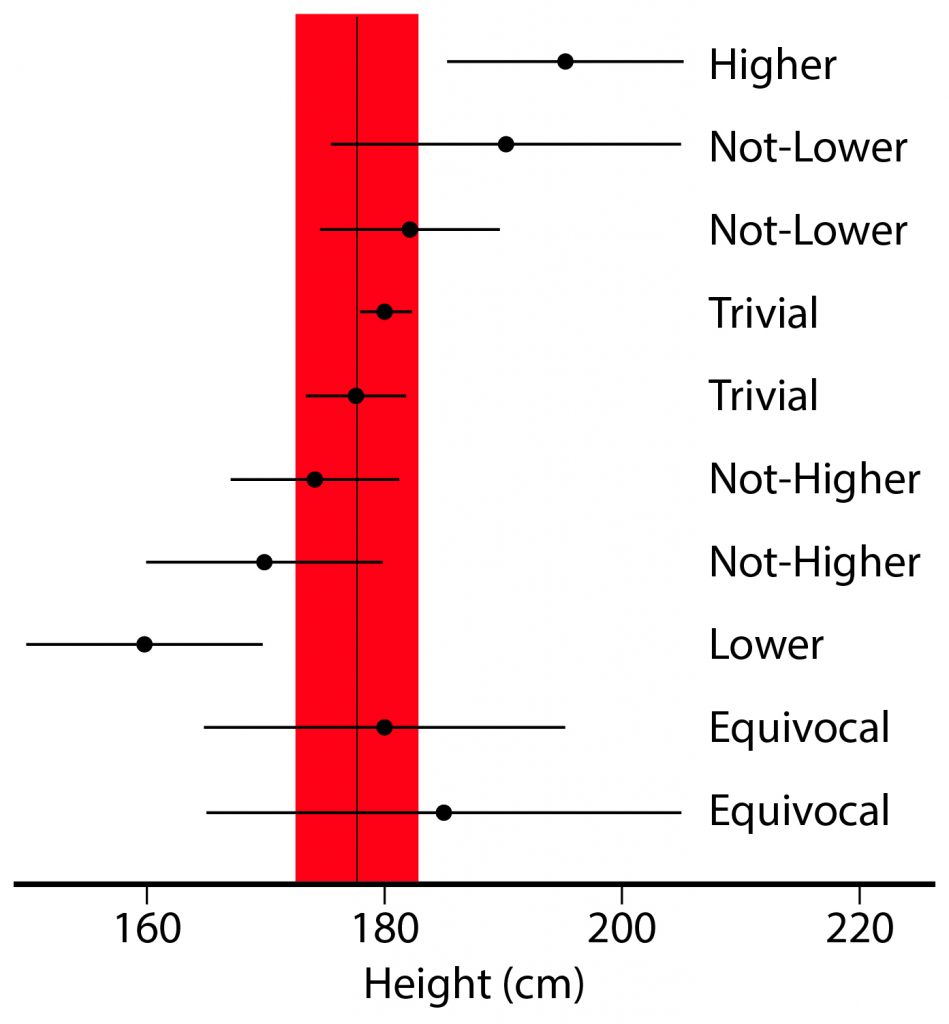
Al calcular el SWC de un atleta, debemos tener en cuenta 3 puntos:
- La percepción, basada en la experiencia, puede ser utilizada para el SWC. Por ejemplo, en la prueba del IMTP, los cambios de menos de 5N son, probablemente, sólo ruido.
- El error de medición es crucial para identificar la señal y el ruido. Por ejemplo; si el TE es 5N para el IMTP, la SWC no puede ser inferior al doble de ese valor, de lo contrario, la incertidumbre es demasiado grande para diferenciar entre los cambios reales y la variabilidad.
- Si realizamos la prueba a un grupo de atletas, podemos multiplicar 0,2 veces el SD de los atletas para obtener el SWC, y 0,3 si el conjunto de datos se toma de una prueba múltiple individual.
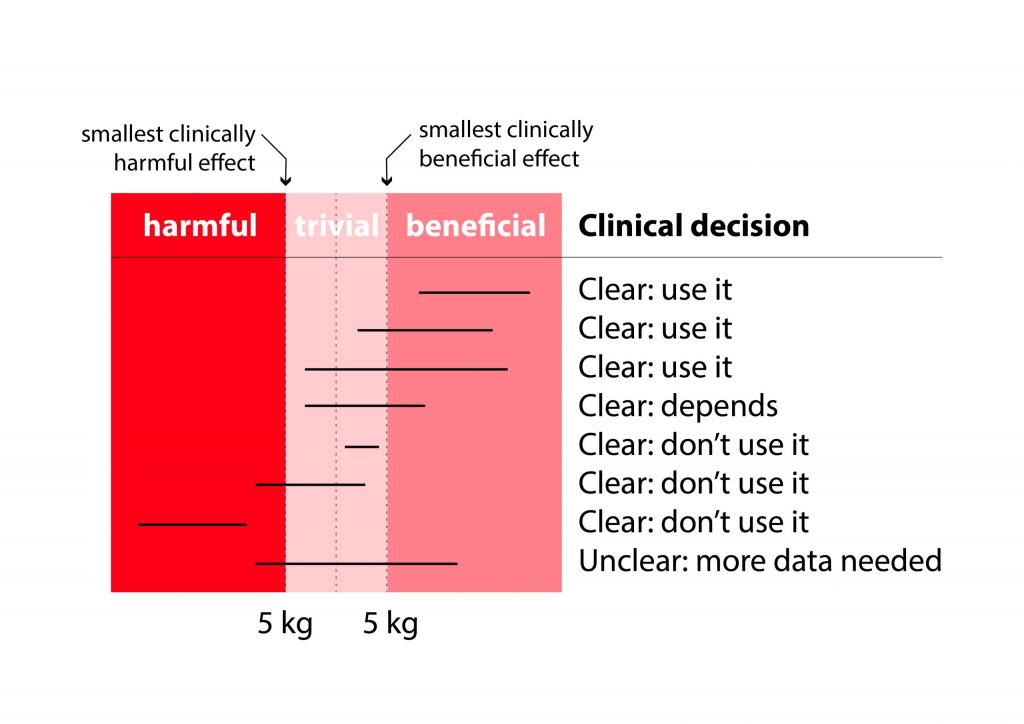
Por ejemplo; Cualquier aumento o disminución en un atleta de 1RM superior a 5 kg se considera relevante, mientras que todos los cambios inferiores a 5 kg son demasiado pequeños para ser de relevancia práctica.
A medida que el intervalo de confianza (distribución) se aleja más de la zona trivial (ya sea a una zona beneficiosa o perjudicial), aumenta la probabilidad de que se produzca un efecto verdadero.
Aplicaciones prácticas
Ahora tenemos una forma de calcular el 1RM de nuestros atletas, que puede ser implementada incluso en los sets de calentamiento. Usando pesos submáximos y rastreando la velocidad concéntrica, podemos crear un método donde podamos rastrear nuestro 1RM diariamente, sin fatigarnos, sin perder tiempo y sin afectar la sesión de entrenamiento.
Mezclarlo con el IBM puede ser un modelo poderoso capaz de darnos información valiosa sobre la probabilidad de mejorar o disminuir nuestro 1RM, sin siquiera medirlo.
La siguiente imagen es de una hoja de cálculo tomada de Mladen Jovanovic. Recomendamos encarecidamente a todo el mundo que siga su trabajo porque, probablemente (sin calcular el IBM), es uno de los más disruptivos, innovadores y útiles en el campo.
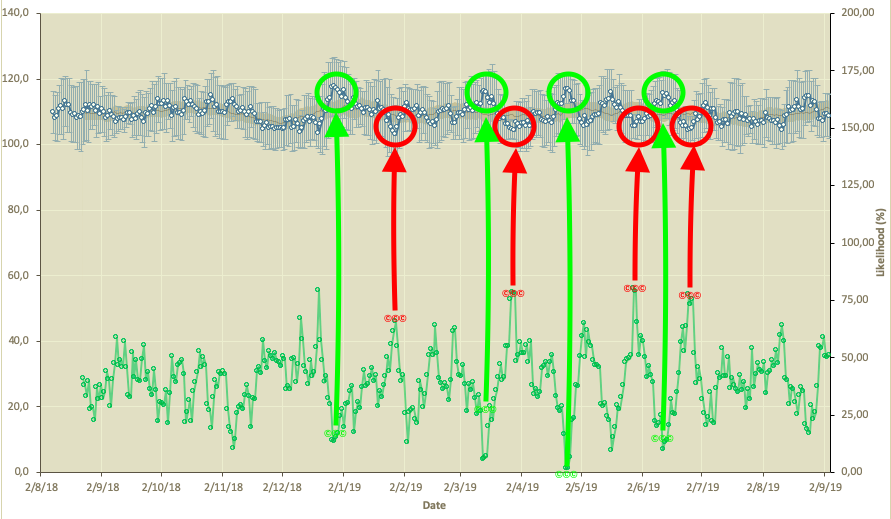
El uso de este enfoque puede ayudar tanto a evaluar el efecto de diferentes aspectos del entrenamiento como el volumen, la frecuencia, la densidad y la carga en el “resultado” (1RM), como a ser utilizado como una herramienta de preparación.
Como vimos, seguir con precisión el progreso de un atleta es una tarea compleja. Con toda la información aquí vertida, sin duda tendrás mejores herramientas para poder aplicar en el entrenamiento.
¿Querés aprender más? Elegí alguno de nuestros cursos y pagalo con un 20% de descuento si ya sos miembro. ¿Aún no sos miembro? ¡Dale clic acá y sumate!







